What is a Tensor Rank and Tensor Shape - TensorFlow

In this article, we will learn about Tensor Ranks and Tensor Shapes.

We know a tensor is an n-dimensional array. So, Rank is defined as the number of dimensions of that tensor. And, Tensor Shape represents the size of the each dimension.

Dimension levels

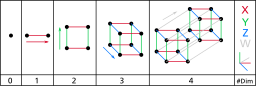
A tensor with rank 0 is a zero-dimensional array. The element of a zero-dimensional array is a point. This is represented as a Scalar in Math and has magnitude.

Eg: s = 48.3

Shape - []

A tensor with rank 1 is a one-dimensional array. The elements of the one-dimensional array are points on a line. This line has magnitude, direction. and is represented as Vector in Math. Vector has n entries.

Eg: v = [1, 9, -6, 7, 0]

Shape - [5]

A tensor with rank 2 is a two-dimensional array. The elements of the two-dimensional array are lines on a surface. This surface is represented as a Matrix in Math and has two coordinates. The Matrix contains n x n entries.

Eg: m = [[2.4, 5.1], [3.3, 7.9], [8.5, 6.1]]

Shape - [3, 2]

A tensor with rank 3 is a three-dimensional array. The elements of the three-dimensional array are surfaces of a cube. This is represented as a 3-Tensor in Math and has three coordinates. 3-Tensor has n x n x n entries.

Eg: t = [[[2, 5, 6], [5, 3, 3], [6, 7, 8]], [[0, 0, 1], [9, 7, 9], [2, 3, 6]], [[4, 8, 2], [1, 0, 8], [4, 4, 0]]]

Shape - [3, 3, 3]

You can continue increasing the entries to create a 4-Tensor, 5-Tensor, .... n-Tensor. n-Tensor has n x n x n x n .... n entries, while it's shape is [n, n, n, n, n, ... n]

Below is the code snippet that creates tensors with different ranks and shapes. Play with it.

Popular posts from this blog

Create Assets Folder, Add Files and Read Data From It

Image
Sometimes, we need to read the data stored in the files during runtime and want to make sure the data is not tampered by the Android build system. In this article, we will take a look at how to create the assets folder using Android Studio and read the stored data from it. First, Right-click on the module name or the package name. This opens an option window where we need to select the Assets Folder option by hovering over New and then on the Folder option. Now, we will see a window where we change the folder location and the source set. Change the values if necessary otherwise keep the defaults and click Finish. It may trigger a Gradle Sync. Irrespective of the sync, the Assets folder is created and is visible in the module. Now, Right-click on the Assets folder and click on the File option by hovering over the New option. Enter the name of the file name and click Enter to create the file. The file with the name user_details.json is created under the assets folder. Add some JSON...
Read more

How to Read Metadata from AndriodManifest File

Metadata tags are key-value pairs and one of the decent ways to access the API keys from the libraries. They are added to the AndroidManifest.xml under the application tag and are available through the PackageManager . If you have worked with third-party libraries or even with App shortcuts, Downloadable Fonts, Firebase MLKit, you may have come across metadata tags. In the article, let’s add the metadata tags to the app module’s Manifest file and read the metadata key-values and the key-resource from a library module both in kotlin and java. Add meta-data: Add metadata to the app module's AndroidManifest.xml file under the application tag. You can add as many metadata elements as you want and you can also add metadata under the activity, service, broadcast receiver, content provider tags. <meta-data android:name= "com.gsrikar.library.LIBRARY_ACCESS_KEY" android:value= "masndfiu4er9funwikesd" /> <meta-data and...
Read more

Add Spacing to Recycler View Linear Layout Manager Using Item Decoration

Image
In this article we will learn about, item decoration in Android and how we can use it to add even spacing between the child items. A RecyclerView without spacing will look like the image below but in most cases, we want to add spacing between the items. [You can see there are no margins between the views and only elevation] A more traditional option is adding margins in the list item xml file. If we take this route, we will soon end up with uneven spacing issues with vertical margins. [There are even left, right, top, bottom margins for all the rows except the last item in the first image and in the subsequent image, the top margin for the first item is half of the other items] The best way is to add the ItemDecoration to the RecyclerView as it affects the individual items and you can have more control over them. Kotlin: /** * Add vertical, horizontal spacing to the recycler view */ class DefaultItemDecorator(private val horizontalSpacing: Int, ...
Read more

Run the Emulator directly in Android Studio

Image
In Android Studio 4.1, a minor feature is released to reduce the screen (or window) switching between Android Studio and the Emulator. Using this feature, we can now run the Emulator directly inside the Android Studio. We can make the changes to the code and see the changes reflect in the emulator in the same window similar to layout XML and its preview. To achieve this, open the Preferences window and select the Emulator menu item under the Tools expandable menu. Here we can check the option Launch in a tool window and click OK . Now run the Emulator to see it inside the Android Studio window.
Read more

How to Change Material Chip Text Size, Text Style and Font

Chips in Android is a Material Design Component used primarily for actions or choice or during filters or as an input. The attributes like textColor , textStyle and fontFamily are ignored when added to the Material Chips directly. We need to modify these values using textAppearance . <com.google.android.material.chip.Chip android:id="@+id/maleChip" style="@style/Widget.MaterialComponents.Chip.Choice" android:layout_width="wrap_content" android:layout_height="wrap_content" android:checkable="true" android:layoutDirection="locale" android:text="@string/chip_text_male" android:textAppearance="@style/AppTheme.GenderChip" android:textColor="@color/colorWhiteText" app:chipBackgroundColor="@drawable/select_chip" app:chipEndPadding="@dimen/chip_horizontal_margin" app:chipStartPadding="@dimen/chip_horizontal_margin...
Read more